|
ESTONIAN SOCIAL SCIENCE ONLINE |
|
Nimetus struktuurivõrrandite mudelite analüüs ei viita ainult ühele statistilisele meetodile, vaid omavahel seotud statistiliste protseduuride perele. Kuid sellele lähenemisele on antud hulk erinevaid nimetusi, näiteks paralleelsete terminitena on kasutusel ka kovariatsiooni struktuuri analüüs, kovariatsiooni struktuuri mudelid, latentsete tunnuste analüüs ning põhjuslikud mudelid. (Kline 1998:7)
Struktuurivõrrandite mudelite tähtsamad karakteristikud (Kline 1998:8):
Struktuurivõrrandite mudelite analüüs on kogum erinevatest omavahel seotud statistilistest meetoditest. Seega puudub tal ka ühene algallikas. Osa struktuurivõrrandite mudelite analüüsist, mida praegu tuntakse kirjeldava faktoranalüüsi nime all, töötati välja Charles Spearman’i (1904) poolt eelmisel sajandivahetusel. Mõned aastad hiljem (1921, 1934) tutvustas geneetik Sewell Wright teeanalüüsi põhialuseid. (Kline 1998:13-14)
Alles 1960-tel pälvisid Sewell Wright’i teeanalüüsi ideed ka sotsiaalteadlaste tähelepanu. Esimestena tutvustasid teeanalüüsi kasutamise võimalusi sotsiaalteadustes Blalock (1964) ja Duncan (1966). Üks olulisemaid valdkondi, kus struktuurivõrrandite metoodikat algselt kasutati oli ‘sotsiaalse staatuse saavutamise protsess’. Nimelt uuriti, millised faktorid mõjutavad inimest töö- ja karjäärivalikul kõige enam. Uuringus, mis viidi läbi Duncani jt teadlaste poolt, vaadeldi faktoreid, mis mõjutasid hariduse omandamist ja hilisemaid karjäärivalikuid. Uuringu käigus vaadeldi selliseid faktoreid nagu perekonna sotsiaalne klass, eelnevad akadeemilised saavutused ja sotsiaalne toetus lähedastelt. Nendes mudelites olid sõltuvateks tunnusteks hariduse omandamine (õpitud aastate arv, saavutatud tase või kraad jne) ja tööalane staatus. (Maruyama 1998:17)
Ettekujutuse struktuurivõrrandite mudelite kasutamisest sotsiaalsete protsesside
hindamisel annab joonisel 1 toodud
teemudel.
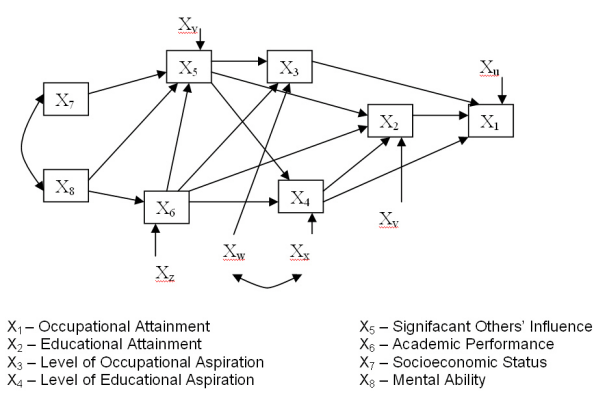
Joonis 1: Sewell–Haller-Ohlendorf Model of Educational and Occupational Attainment
Allikas: W. H. Sewell, A. O. Haller ja G.W. Ohlendorf, The Educational and Early Occupational Status Attainment Process: Replication and Revision. American Sociological Review 35 (December 1970): 1023
Teediagrammilt on näha, et vanemate sotsiaal-majanduslik staatus (X7) mõjutab kaudselt laste hariduslikke saavutusi (X2) ja tööalaseid püüdlusi (X3). Need omakorda mõjutavad otseselt laste hilisemaid tööalaseid saavutusi (X1). Teiste sõnadega aitab vanemate kõrgem sotsiaal-majanduslik staatus kaasa laste parema hariduse saamisele ja kujundab nende kõrgemad tööalased ootused ja püüdlused, mis omakorda viivad suurematele tööalastele saavutustele.
(http://www.nd.edu/~rwilliam/zsoc593/spring2003/lectures/l14.pdf )
Eelnevaid teadmisi kirjeldava faktoranalüüsi ja teeanalüüsi vallas asusid 1970-te alguses edasi arendama kolm teadlast K.G.Jöreskog, J.W.Keesling ja D.E.Wiley. Nende edasiarendusest ongi välja kasvanud struktuurivõrrandite mudelite teooria. Üks esimesi arvutiprogramme selliste mudelite analüüsimiseks töötati samuti välja 1970-tel K.G.Jöreskog’i ja D.Sörbom’i poolt. Selleks on ka tänapäeval laialt kasutatav LISREL (Linear Structural Relationships). Järgnevatel aastakümnetel töötati struktuurivõrrandite mudelite analüüsimiseks välja veel mitmeid teisi arvutiprogramme ja meetodit ennast hakati laialdaselt kasutama ka muudel elualadel, näiteks spordimeditsiinis, arengupsühholoogias ja geneetikas. (Kline 1998:14)
On lineaarne analüüsimeetod, kus sõltuvat tunnust mõjutavad mitu argumenti, mis võivad ka omavahel korreleeritud olla. Argumentide vaheline korrelatsioon muudab regressioonimudelite ja struktuurivõrrandite mudelite analüüsi huvipakkuvaks, kuid toob uurijale kaasa ka hulgaliselt probleeme.
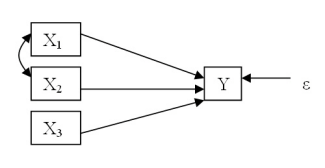
Mitmese regressioonanalüüsi korral võivad hinnangud argumentide vahelise tugeva korrelatsiooni tõttu muutuda ebastabiilseks ja tekivad multikollineaarsuse probleemid. Kuid struktuurivõrrandite mudelite analüüs võimaldab hinnata ka mudeleid, kus argumentide vahelised korrelatsioonid on küllaltki suured. (Maruyama 1998:61)
Üldiselt on mitmese regressioonanalüüsi roll struktuurivõrrandite mudelite koostamisel piiratud. Põhiliselt kasutatakse regressioonanalüüsi esialgsete andmete ettevalmistamisel ja eelanalüüsil. Samuti saab meetodit kasutada teatud teeanalüüsi mudelite hindamisel, kui kaasatud ei ole latentseid tunnuseid ning mõõdetud tunnuste jääkliikmed ei ole korreleeritud. Üldiselt kasutatakse stuktuurivõrrandite mudelite hindamisel vähimruutude meetodi asemel suurima tõepära hinnanguid.
Kui struktuurivõrrandite mudelisse ei kaasata latentseid tunnuseid ning põhjuslikud mõjud on ühesuunalised, siis on tegemist meetodi erijuhuga, mida tuntakse teeanalüüsi nime all. (Kline 1998:50)
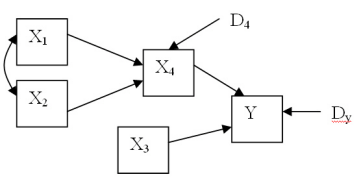
Erinevalt mitmesest regressioonanalüüsist võimaldab teeanalüüs lisaks otsestele mõjudele uurida ka kaudseid mõjusid mudelis. Toodud näite korral mõjutavad sõltuvat tunnust Y otseselt tunnused X3 ja X4. Kaudselt mõjutavad tunnust Y läbi tunnuse X4 ka tunnused X1 ja X2. Kogu valitud argumentide mõju tunnusele Y saame kui liidame kõik otsesed ja kaudsed mõjud.
Kui regressioonanalüüsi korral pole lõplikus mudelis olevate argumentide arv enne analüüsi algust teada, siis teeanalüüsi korral alustatakse analüüsi uurija hüpoteesidele vastava struktuurimudeli kirjeldamisest. Mudeli kirja panemiseks on kaks võimalust – mudeli saab konkreetseid tähistusi kasutades üles joonistada või esitada hüpoteesid võrrandite süsteemina. Struktuurivõrrandite mudelite jaoks loodud statistikapakettides on olemas mõlemad võimalused, kusjuures kasutaja poolt graafiliselt kujutatud mudeli põhjal on programm võimeline automaatselt sellele vastava võrrandite süsteemi kirja panema. (Kline 1998:53)
Struktuurivõrrandite mudelite analüüs kasutab mudelite ülesmärkimisel suures osas teeanalüüsi jaoks välja töötatud märgistusi, lisaks on keerulisemate seoste jaoks kasutusele võetud ka ainult struktuurimudelile omaseid tähistusi. Siiski ei ole mudeli graafilisel esitamisel ühtset süsteemi välja kujunenud ning uurijad võivad kasutada erinevaid sümboleid.
Kirjeldava faktoranalüüsi meetod on mõeldud sisult lähedaste mõõdetud tunnuste koondamiseks faktoriks. Kirjeldava faktoranalüüsi abil on võimalik esitada mõõdetud tunnused ühtsete faktorite ja nende juurde kuuluva omapära dispersioonina. Struktuurivõrrandite mudelite vaatenurgast võimaldab kirjeldav faktoranalüüs mõõdetud tunnustega teeanalüüsi mudelite juurest edasi liikuda teemudelite juurde, kus ühe huvipakkuva faktori määravad mitu indikaatorit. Siiski ei ole hiljem sellisel viisil laiendatud teeanalüüsi mudelit võimalik hinnata tavapärase vähimruutude regressiooni meetodiga. (Maruyama 1998:132-133)
Kirjeldava faktoranalüüsi mudelis on faktorid omavahel sõltumatud ning üks indikaatortunnus võib olla seotud mitme faktoriga. Kuid struktuurivõrrandite mudelite korral ei paku olukord, kus faktorite vahelised seosed puuduvad, meile huvi. Pigem eeldame, et ka faktorid on omavahel korreleeritud.
Kline’i hinnangul on kinnitava faktoranalüüsi mudel sotsiaalteaduslikus kirjanduses kõige enam kasutatud mudel. Kinnitava faktoranalüüsi mudelis on faktorid omavahel seotud ning erinevalt kirjeldava faktoranalüüsi mudelist on iga indikaatortunnus seotud vaid ühe faktoriga.
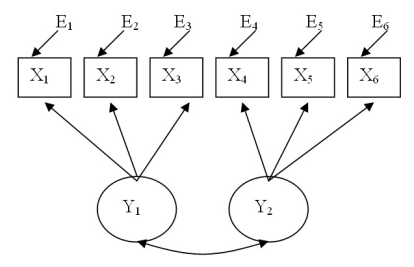
Joonis 4. Näide kinnitava faktoranalüüsi mudelist
Toodud mudel sarnaneb teemudelile oma ülestähenduselt. Sirged ühesuunalised nooled viitavad otsestele põhjuslikele mõjudele faktorite ja indikaatorite vahel. Kahesuunaline nool faktorite vahel viitab nende võimalikule korrelatsioonile mitte vastastikule mõjule. Otsesed mõjud joonisel viitavad faktorite kaudsele mõjule indikaatorite suhtes ehk sellele, kui suur osa faktori hajuvuse kirjeldamisest kajastub just selle indikaatori kaudu. Seega võib toodud mõõtmismudelit vaadelda kui struktuurimudelit, kus latentsete tunnuste eeldatavat kaudset mõju hinnatakse indikaatorite kaudu.
Kinnitava faktoranalüüsi mudeli abil hinnatakse faktorite dispersioone ja kovariatsioone, indikaatorite mõõtmisvigu ning faktorite ja indikaatorite vahelisi seoseid (faktorlaadungeid). Kinnitava faktoranalüüsi korral kasutatakse hindamisel põhiliselt suurima tõepära hinnanguid. (Kline 1998:238-239)
Struktuurivõrrandite mudelite analüüs
Kõige üldisemal kujul on struktuurivõrrandite mudel ristmudel (hybrid model) mõõtmismudelist ja struktuurimudelist. Sarnaselt teeanalüüsile võimaldab ristmudel kontrollida hüpoteese mudelis esinevate tunnuste vaheliste otseste ja kaudsete mõjude kohta. Erinevalt teeanalüüsist ühendab ristmudel mõõdetud tunnused ühtseteks konstruktsioonideks ja võimaldab hinnata põhjuslikke seoseid nende konstruktsioonide ehk latentsete tunnuste vahel. (Kline 1998:244)
Ristmudeli ülesehitust iseloomustab järgmine joonis.
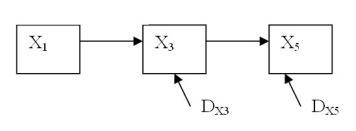
(a) Teemudel
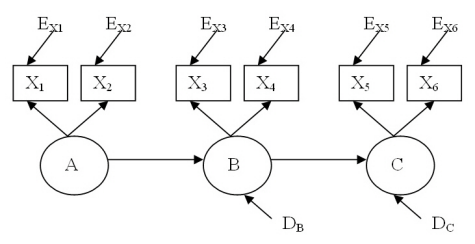
(b) Ristmudel
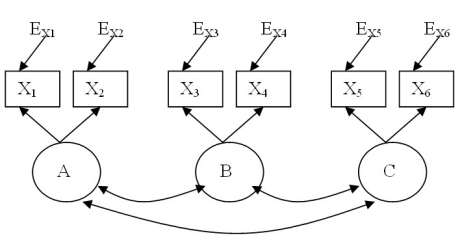
(c) Kinnitava faktoranalüüsi mudel
Joonis 5. Näide teemudeli ja kinnitava faktoranalüüsi mudeli sidumisest ristmudeliks.
Mudeli (a) korral on tegemist mõõdetud tunnustega struktuurivõrrandite mudeli
ehk teemudeliga, millest ka eelnevalt pikemalt juttu oli. Mudel (b) on tüüpiline
ristmudel nii struktuuri- kui ka mõõtmiskomponentidega. Mõõtmismudelit esindavad
need samad kolm tunnust teemudelist (X1, X3, X5),
mis nüüd koos teiste tunnustega on latentsete tunnuste indikaatoriteks. Igale
mõõdetud tunnusele vastab mõõtmisviga. Ristmudeli struktuurikomponenti esindavad
samasuunalised põhjuslikud seosed nagu teemudelis, kuid siin juba latentsete
tunnuste vahel.
Mudel (c) esindab tüüpilist kinnitava faktoranalüüsi mudelit, kuid erinevalt ristmudelist pole latentsete tunnuste vahelised seosed selle mudeliga üheselt määratud (Kline 1998:245).
Järgnevalt toon näite struktuurivõrrandite mudeli leidmisest reaalsetel andmetel. Analüüsi aluseks olid Statistikaameti leibkonna eelarve uuringu andmed aastast 2000. Erinevate leibkonda ja leibkonnapead iseloomustavate tunnuste alusel oli eesmärgiks leida leibkonna majanduslikku olukorda mõjutavad faktorid ja hinnata seoseid nende vahel. Analüüsi teostamisel kasutati statistikaprogrammi SAS (Statistical Analytical System) abi.
Esialgne andmestik sisaldas 2343 lastega leibkonna andmeid ja neil mõõdetud 49 tunnust. Tunnuste hulgas oli nii pidevaid kui ka järjestustunnuseid.
Kasutatavatest tunnustest parema ülevaate saamiseks jagasin need gruppidesse:
Analüüsi kaasatud tunnuste põhjal oli eesmärgiks leida kompaktne struktuurivõrrandite mudel, mis kirjeldaks leibkonna majanduslikku olukorda. Tunnuste selekteerimisel kasutasin kirjeldava- ja kinnitava faktoranalüüsi võimalusi. Pärast struktuurimudeli sobivuse kontrolli kinnitava faktoranalüüsi abil oli mudelis 14 indikaatorit, mida kirjeldasid 3 faktorit – faktor F3 peegeldab leibkonna üldisi majanduslikke näitajaid – elukoht, kodune keel, liikmete arv, faktor F2 sisaldab infot leibkonnaliikmete aktiivsuse kohta ning faktor F1 on tugevalt seotud leibkonna sissetuleku ja majandusliku olukorra näitajatega. Sama faktoriga seotud tunnuste vahel oli mudelis hindamiseks 3 korrelatsiooniseost.
Viimases etapis oli eesmärgiks hinnata faktoritevahelisi seoseid. Saadud mudelis oli kolm sisuliselt väga lihtsalt interpreteeritavat faktorit, mistõttu seosed faktorite vahel oli võimalik enne hindama asumist loogiliselt paika panna. Leibkonna elukoht ja liikmete arv mõjutavad leibkonnapea ja teiste liikmete aktiivsust ja sissetulekut, aktiivsete liikmete arv aga sissetulekute suurust ja hinnanguid majanduslikule olukorrale. Kokkuvõttes mõjutab faktor F3 faktorit F2 ja koos mõjutavad nad leibkonna majandusliku olukorra faktorit F1.
Kogu ristmudeli hindamisel lisandus mudelisse veel 4 korrelatsiooni mõõdetud tunnuste vahele. Lõplik mudel leibkonna majandusliku olukorra hindamiseks koos faktorite vaheliste seoste ning lisatud korrelatsioonidega on toodud joonisel 6.
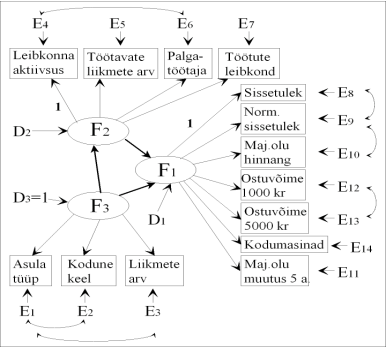
Joonis 6. Struktuurimudel leibkonna majandusliku olukorra hindamiseks.
Pärast mudeli lõplikku hindamist on võimalik välja kirjutada faktorite vahelisi seoseid kirjeldavad võrrandid:
F1= 0,55(F2) – 0,27(F3) + 0,75
F2 = –0,22 (F1) + 0,98
Leibkonna majandusliku olukorra ehk faktori F1 kirjeldatus on ligikaudu 45%
Leibkonna aktiivsuse ehk faktori F2 kirjeldatus on 5%.
Seega oleme leibkonna majandusliku olukorra hindamiseks saanud kompaktse 14 mõõdetud ja 3 latentse tunnusega mudeli. Leitud mudel on suhteliselt hea , kõik esitatud seosed mudelis on olulised ja hinnatud ning vaadeldud sobivusindeksid ületavad empiirilist kriteeriumi. Leibkonna aktiivsuse faktor ning taustafaktor kirjeldavad leibkonna majandusliku olukorra faktorist ligikaudu 45%. Samas võib leiduda teisigi mudeleid, mis nende andmetega hästi sobivad. Niisiis pakub siin esitatud mudel vaid ühe võimaluse leibkonna majanduslikku olukorda mõjustavate faktorite hindamiseks (Themas 2003)
Struktuurivõrrandite mudelite analüüs on väga üldine ja võimas mitmese statistilise analüüsi tehnika, mille eesmärgiks on mudelis esinevate põhjuslike sõltuvusseoste hindamine. Meetod sisaldab endas teisi laialt kasutatavaid analüüsi meetodeid, näiteks teeanalüüsi, regressioonanalüüsi, kirjeldavat ja kinnitavat faktoranalüüsi jm. Struktuurivõrrandite mudelite koostamine on aprioorne ning nõuab uurijalt eelnevaid kogemusi ja teadmisi põhjuslike seoste määramisel. Tegemist on suure valimi analüüsi meetodiga, hinnangute stabiilsuse ja korrektsuse huvides peaks kasutatav valimi sisaldama rohkem kui 200 objekti. Struktuurivõrrandite mudelite koostamiseks on olemas mitmeid kasutajasõbralikke arvutiprogramme (LISREL, R, SAS jne). Näitena toodud struktuurimudel leibkonna majandusliku olukorra hindamiseks on saadud Eesti Statistikaameti leibkonna eelarveuuringu andmeid ja statistikaprogrammi SAS kasutades.
Viited
Kline, Rex B. Principles and Practice of Structural Equation Modeling, The Guilford Press, New York, 1998.
Maruyama, Geoffrey M. Basics of Structural Equation Modeling, SAGE Publications, 1998.
Themas, Aivi. Struktuurimudeli koostamine leibkonna majandusliku olukorra hindamiseks. Bakalaureusetöö. Tartu, 2003.
Intro to Path Analysis - http://www.nd.edu/~rwilliam/zsoc593/spring2003/lectures/l14.pdf